차원 축소 알고리즘
차원 축소 알고리즘은 matrix factorization과 neightbor graph 2가지로 나눌 수 있는데,
t-SNE와 UMAP은 neighbor graph에 해당합니다.
PCA
- matrix factorization 을 base 로 함 (공분산 행렬에 대해서 svd 등)
- 분산이 최대인 축을 찾고, 이 축과 직교이면서 분산이 최대인 두번째 축을 찾아 투영시키는 방식(공분산 행렬의 고유값과 고유벡터를 구하여 산출)
- 단점 : 선형 방식으로 정사영하면서 차원의 축소 -> 군집된 데이터들이 뭉게지는 단점

t-SNE : t-distributed Stochastic Neighbor Embedding
t-SNE는 데이터의 manifold를 잘 학습하여 데이터의 차원을 축소하거나 의미있는 특징 추출 혹은 데이터를 가시화하기 위한 manifold learning의 일종


- neighboring graph 를 base 로 함
- Local neighbor structure를 보존(고차원의 벡터의 유사성이 저차원에서도 유사도록 보존
- t 분포를 이용해 하나의 기준점을 정하고 모든 다른 데이터와 거리를 구한 후 그 값에 해당하는 t 분포 값을 선택, 값이 유사한 데이터끼리 묶어줌
- t 분포(t-distribution)는 스튜던트 t 분포(Student's t-distribution)와 동일한 용어
t-SNE 장점
t-SNE는 특징을 추출하거나, 데이터의 특징을 가시화하기에 아주 robust한 알고리즘
- 기존 PCA (주성분 분석)과 같은 선형 변환은 데이터를 저차원으로 임베딩하여 가시화할 때 겹쳐서 뭉게지는 부분 발생 -> unsupervised learning의 일종인 t-SNE를 사용한다면 뭉개지는 문제점 해소
- 또한 저차원 임베딩을 t 분포 기반으로하기 때문에 기존 SNE 방법과 같이 저차원 임베딩에서 정규분포(가우스 분포)를 사용했을 때 나타나는 crowding 문제점이 해결됩니다(특정 거리 이상부터는 학습에 반영이 되지 않는 문제점).
- 또한 다른 차원 축소 알고리즘에 비해 hyperparameter의 영향이 적고 이상치(outlier)에 둔감하다는 장점
t-SNE 단점
1. 차원 축소의 시간이 너무 오래걸림
1) 데이터 개수에 따른 연산량 증가
데이터의 개수가 n개라면 연산량은 n의 제곱만큼 늘어남 -> 시간이 너무 오래 걸림 -> UMAP으로 해결
2) 높은 차원의 데이터를 순차적으로 차원 축소
너무 높은 차원을 가진 데이터를 바로 2, 3차원으로 축소하는 것이 불가능
→ 보통 128차원 raw 데이터 → autoencoder(reduce 32 demention) 줄어든 잠재 변수(latent variable) 구하기
→ 32차원을 2, 3차원으로 축소하기 위해 t-SNE를 사용
→ 보통 50차원 이내로 raw data 압축 이후 t-SNE 이용한다고 함
2. 매번 돌릴 때마다 다른 시각화 결과가 나옴(training 과 prediction 을 동시에 수행)
→ 학습에 활용할 수 없게 됨 혹은 seed 고정으로 결과값 통일
3. 저차원 임베딩 시 정보손실 발생 -> 데이터 왜곡의 가능성
UMAP - Uiform Manifold Approximation and Projection
- neighboring graph 를 base로 함
- 가장 좋은 성능을 내는 알고리즘이라고 알려짐
- (UMAP is arguably the best performing as it keeps a significant portion of the high-dimensional local structure in lower dimensionality (https://towardsdatascience.com/topic-modeling-with-bert-779f7db187e6))
- 방법
- high dimension space 에서의 데이터를 graph로 만들고, low dimension 으로 graph projection한다 (이 전 과정이 유효하다고 수학적으로 증명돼있다고 함)

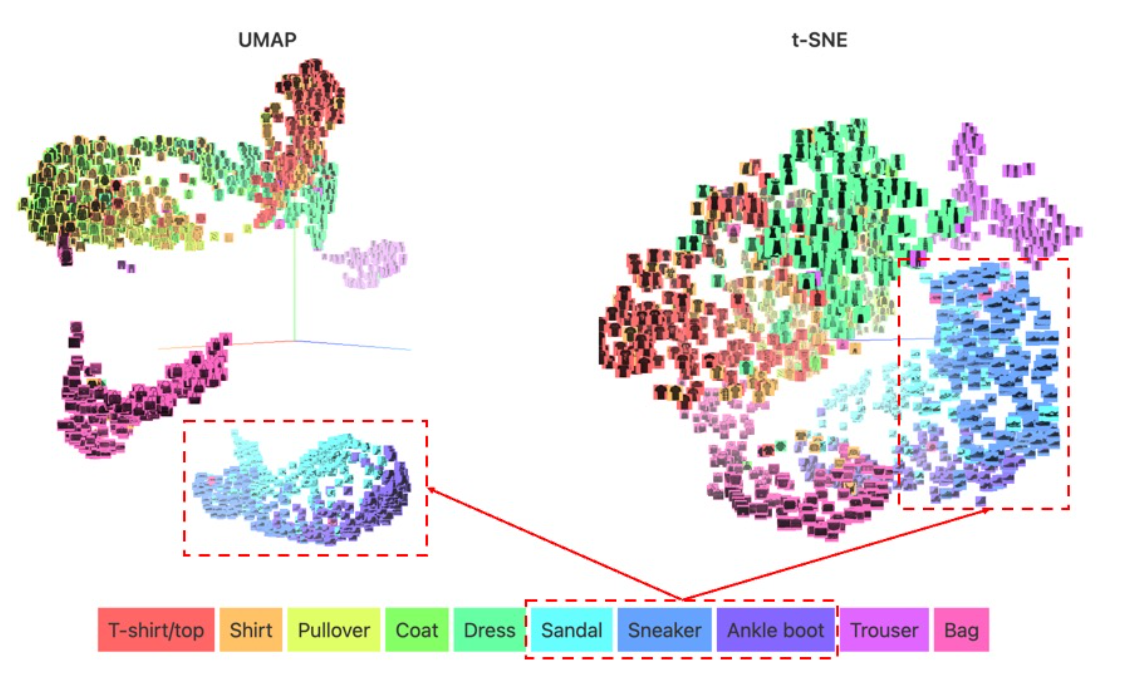
UMAP 장점
- 빠르다
- embedding 차원 크기에 대한 제한이 없어서 일반적인 차원 축소 알고리즘으로 적용 가능함
- global structure 를 더 잘 보존(시각화도 더 예쁘게 잘 된다)
- 탄탄한 이론적 배경 - 리만 기하학 & 위상수학에 기반
UMAP 단점
- Hyperparameter(머신러닝/딥러닝의 변수 - 모델의 성능에 영향)의 영향을 크게 받는다.
- 저차원으로 임베딩되어 가시화 된 결과에서 각 데이터간 거리 ≠ 실제 데이터 간 거리
- 저차원 임베딩 시 정보손실에 의한 데이터 왜곡
참고 및 출처
https://ljm565.github.io/contents/ManifoldLearning2.html
https://data-newbie.tistory.com/295
https://pair-code.github.io/understanding-umap/
'머신러닝딥러닝 > 딥러닝' 카테고리의 다른 글
| [딥러닝] 인공신경망 패션아이템 분류 - 혼자공부하는 딥러닝 (0) | 2022.11.30 |
|---|---|
| 코사인 유사도(Cosine Similarity)vs 유클라디안 유사도(Euclidean Similarity)vs 자카드 유사도(Jaccard Similarity) (0) | 2022.11.28 |
| 딥러닝(Deep Learning) #16 - RNN & CNN (0) | 2022.04.17 |
| 딥러닝(Deep Learning) #15 - RNN (0) | 2022.04.15 |
| 딥러닝(Deep Learning) #14 - CNN (0) | 2022.04.15 |




댓글