미분

x 값이 아주 미세하게 움직일 때, y변화량을 구한 뒤, 이를 x변화량으로 나누는 과정
경사하강법(Gradient decent)
미분의 기울기를 이용해 기울기가 0인 한 점(m)을 찾는 방법

위 그래프에서 오차가 가장 적은 지점 a=m
m과 같은 기울기 a를 찾았을 때 오차가 가장 적어짐
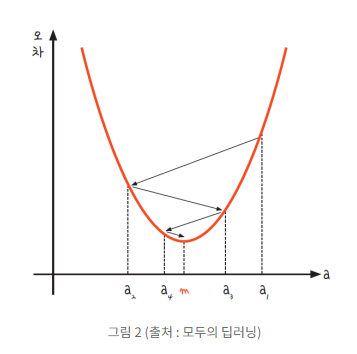
a=m에 가까운 지점을 경사를 하강시켜 찾아가는 과정을 경사하강법이라 한다.
시작점 a1의 미분을 구하고, 구해진 기울기의 반대방향으로 이동시킨 뒤 a2를 구한다.
a=0이 아니라면, 과정을 반복하여 기울기가 m = 0 으로 수렴한다.
학습률
경사하강법에서 기울기 반대편으로 이동시킬 때, 얼만큼 이동시킬지 결정하는 값.
학습률을 적절히 바꾸며 최적의 학습률을 찾는 것이 중요한 최적화 과정 중 하나
경사하강법
# x, y 데이터 리스트 제작
data = [[2, 80], [4, 92], [6, 87], [8, 95]]
x_data = [i[0] for i in data]
y_data = [i[1] for i in data]
learn_rate = 0.1
a = tf.Variable(tf.random.uniform([1], 0, 10, dtype=tf.float64, seed=0))
b = tf.Variable(tf.random.uniform([1], 0, 100, dtype=tf.float64, seed=0))기울기 a = 0~10 사이에서 임의 기울기 값 a
y절편 b = 0~100 사이에서 임의 y절편 값 b
임의 a,b값 구하기
tf.Variable() = 변수의 값 정하기
random.uniform() = 임의 수를 생성하는 함수, 최소~최대값 작성가능
ex) random.uniform([1], 0, 100, dtype=tf.float64, seed=0)
0~100사이 임의의 수 1개를 만들어라는 뜻
dtype=tf.float64 : 데이터 형식 실수형(float64)로 설정
seed = 0 : 실행시 같은 값이 나올 수 있게 하는 설정
# 일차방정식 구현
y = a * x_data + b일차방정식 구현
rmse = tf.sqrt(tf.reduce_mean(tf.square(y - y_data)))평균 제곱근 오차식
tf.sqrt(x) : x의 제곱근계산
tf.reduce_mean(x) : x의 평균 계산
tf.square(x) : x제곱을 계산
# tensorflow 버전 1.5 일 때
gradient_decent = tf.compat.v1.train.GradientDescentOptimizer(learn_rate).minimize(rmse)
# tensorflow 버전 2.0 이상일 때
gradient_decent = tf.keras.optimizers.SGD(0.1).minimize(rmse)tensorflow GradientDescentOptimizer() 함수 = keras.optimizers.SGD() 함수는
경사하강법의 결과를 gradient_decent에 할당시킬 수 있다.
# tensorflow 1.5 일때
with tf.compat.v1.Session() as sess:
# 변수 초기화
sess.run(tf.compat.v1.global_variables_initializer())
# 2001번 실행(0번 째를 포함하므로)
for step in range(2001):
sess.run(gradient_decent)
# 100번마다 결과 출력
if step % 100 == 0:
print("Epoch: %.f, RMSE = %.04f, 기울기 a = %.4f, y 절편 b = %.4f" % (step, sess.run(rmse),sess.run(a),sess.run(b)))
# tensorflow 버전 2 이상일 때
lr = 0.03
epochs = 2001
for i in range(epochs): # epoch 수 만큼 반복
y_hat = a * x_data + b #y를 구하는 식을 세웁니다
error = y_data - y_hat #오차를 구하는 식입니다.
a_diff = -(2/len(x_data)) * sum(x_data * (error)) # 오차함수를 a로 미분한 값입니다.
b_diff = -(2/len(x_data)) * sum(error) # 오차함수를 b로 미분한 값입니다.
a = a - lr * a_diff # 학습률을 곱해 기존의 a값을 업데이트합니다.
b = b - lr * b_diff # 학습률을 곱해 기존의 b값을 업데이트합니다.
if i % 100 == 0: # 100번 반복될 때마다 현재의 a값, b값을 출력합니다.
print("epoch=%.f, 기울기=%.04f, 절편=%.04f" % (i, a, b))Session() 함수 = 구동에 필요한 리소스를 컴퓨터에 할당하고 실행시킬 준비
Session.run('그래프명') 형식으로 함수를 구동시킴
global_variables_initializer() = 변수를 초기화하는 함수
앞서 만든 gradient_decent를 필요한 수만큼 실행.
100번마다 RMSE, 기울기, y절편 출력
다중선형회귀
import tensorflow as tf
data = [[2, 0, 81], [4, 4, 93], [6, 2, 91], [8,3,97]]
# 2개의 독립변수 만들기
x1 = [x_row1[0] for x_row1 in data]
x2 = [x_row2[1] for x_row2 in data]
y_data = [y_row[2] for y_row in data]data셋과 x 2개의 독립변수, y 1개의 종속변수 만들기
# 2개의 기울기 구하기
a1 = tf.Variable(tf.random_uniform([1], 0, 10, dtype=tf.float64, seed=0))
a2 = tf.Variable(tf.random_uniform([1], 0, 10, dtype=tf.float64, seed=0))
b = tf.Variable(tf.random_uniform([1], 0, 100, dtype=tf.float64, seed=0))
# 새로운 1차 방정식 만들기
y = a1*x1 + a2*x2 +b독립변수 2개의 기울기와 y 절편 구하기
with tf.compat.v1.Session() as sess:
# 변수 초기화
sess.run(tf.compat.v1.global_variables_initializer())
# 2001번 실행(0번 째를 포함하므로)
for step in range(2001):
sess.run(gradient_decent)
# 100번마다 결과 출력
if step % 100 == 0:
print("Epoch: %.f, RMSE = %.04f, 기울기 a1 = %.4f, 기울기 a2 = %.4f, y 절편 b = %.4f" % (step, sess.run(rmse), sess.run(a1), sess.run(a2), sess.run(b)))실행세션 만들기
Session() 함수 = 구동에 필요한 리소스를 컴퓨터에 할당하고 실행시킬 준비
Session.run('그래프명') 형식으로 함수를 구동시킴
global_variables_initializer() = 변수를 초기화하는 함수
앞서 만든 gradient_decent를 필요한 수만큼 실행.
100번마다 RMSE, x1/x2 기울기, y절편 출력
'머신러닝딥러닝 > 딥러닝' 카테고리의 다른 글
| 딥러닝(Deep Learning) #6 - 퍼셉트론 (0) | 2022.04.12 |
|---|---|
| 딥러닝(deeplearning) #5 - 다항 로지스틱 회귀(Multi_Logistic_Regression) (0) | 2022.04.12 |
| 딥러닝(deeplearning) #4 - 로지스틱 회귀(logistic regression) (0) | 2022.04.12 |
| 딥러닝(deeplearning) #2 - 선형회귀(MSE, RMSE) (0) | 2022.04.11 |
| 딥러닝(deeplearning) #1 - 폐암 수술 환자의 생존율 예측 (1) | 2022.04.11 |




댓글