현대 포트폴리오 이론
현대 포트폴리오 이론 해리 맥스 마코위츠(Harry Max Markowitz)가 1952년 발표한 논문 [포트폴리오 셀렉션]에서 평균-분산 최적화(MVO : Mea-Variance-Optimization)를 제시했다.
평균-분산 최적화(MVO : Mea-Variance-Optimization)란 예상 수익률과 리스크의 상관관계를 활용하여 포트폴리오를 최적화하는 기법을 말한다.
이후 많은 투자자와 학자가 이 모델을 따랐으며, 해리 마코위츠는 1990년에 현대 포트폴리오이론을 창안한 업적으로 노벨 경제학상을 수상한다.
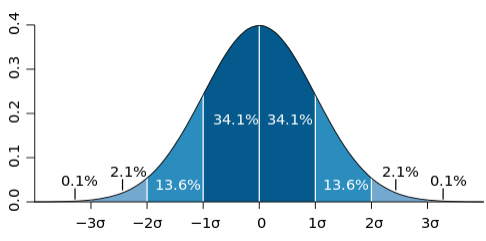
수익률의 표준편차
수익률의 표준편차(Standard deviation of returns)는 자산 가격이 평균값에서 벗어나는 저도인 RISH를 측정하는 방법이다.
주식시장에서 리스크는 주가의 변동성을 말한다.
정규분포 그래프에서 예상 수익률은 평균값인 μ(뮤) 로 나타내고, 리스크는 표준편차인 σ(시그마)로 나타낸다.
어떤 값이 평균에서 떨어진 정도를 편차라고 하며, 각 편차를 제곱에 더한 뒤 평균을 낸게 분산이다.
표준편차는 분산의 제곱근으로 구할 수 있다.
효율적 투자선
효율적투자선(Efficient Frontier)란 현대 포트폴리오 이론의 핵심개념이다.
투자자가 감수할 수 있는 리스크 수준에서 최상의 기대 수익률을 제공하는 포트폴리오 구성을 말한다.
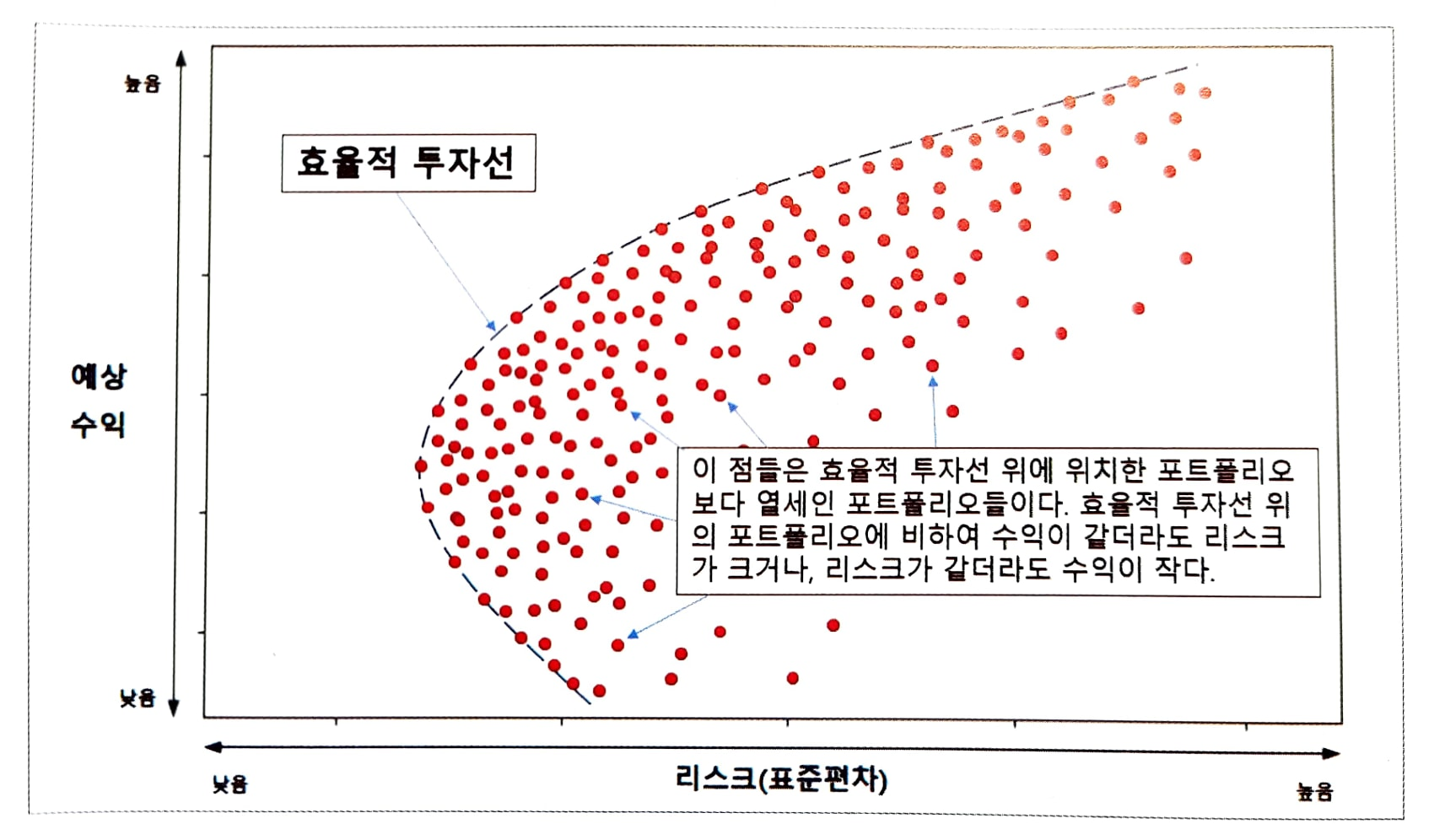
x 축은 risk를 y축은 예상 수익률을 나타낸다.
실선으로 표현된 부분을 효율적 투자선이라고 부르며 붉은 점들은 개별 포트폴리오를 말한다.
효율적 투자선 위에 위치한 포트폴리오는 주어진 리스크에서 최대 수익을 낸다고 볼 수 있다.
효율적 투자선 python구현하기
KOSPI 시총 상위 10 종목으로 효율적 투자선을 구해보려고 한다.
앞서 개발했던 MarKetDB의 일별 시세 조회 API를 이용한다.
삼성전자는 2018년 5월 4일에 액면분할을 ,네이버는 2018년 10월 12일에 액면 분할을 실시했다.
액면분할을 고려하여 DB를 만들지 않았기 때문에 2018년 10월 12일 이후부터 검색기간을 정했다.
시가총액 상위 5종목 일별 시세 데이터 DB에서 가져오는 코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 모듈경로 지정
import sys
sys.path.append(r'C:\Users\kwonk\Downloads\개인 프로젝트\juno1412-1\증권데이터분석\DB_API')
# 모듈 가져오기
import Analyzer
mk = Analyzer.MarketDB()
# KOSPI 시가총액 5위
stocks = ['삼성전자', 'LG에너지솔루션', '삼성바이오로직스', 'SK하이닉스', 'LG화학']
df = pd.DataFrame()
for i in stocks:
df[i] = mk.get_daily_price(i, '2018-10-13', '2022-12-23')['close']
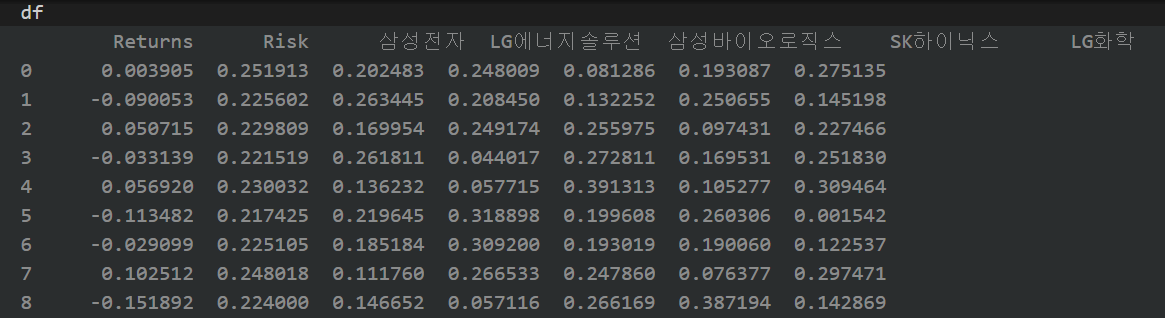
print(df)

시가총액 상위 5종목의 일간 수익률, 연간수익률, 일간리스크, 연간리스크 구하기
# 데이터를 토대로 종목별, 일간 수익률, 연간수익률, 일간리스크, 연간리스크를 구하기
# 5종목 일간 수익률
daily_ret = df.pct_change()
# 5종목 1년간 수익률 평균(252는 미국 1년 평균 개장일)
annual_ret = daily_ret.mean() * 252
# 5종목 연간 리스크 = cov()함수를 이용한 일간변동률 의 공분산
daily_cov = daily_ret.cov()
# 5종목 1년간 리스크(252는 미국 1년 평균 개장일)
annual_cov = daily_cov * 2525종목의 일간 수익률

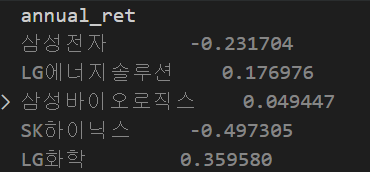
5종목의 연간 수익률
5종목의 일간 리스크 : risk는 cov()함수를 이용한 일간변동률 의 공분산

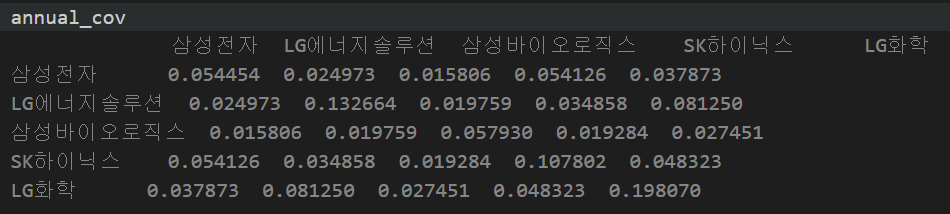
5종목의 연간 리스크
시가총액 상위 5종목 20,000개 포트폴리오 생성 코드
# 시가총액 5순위 주식의 비율을 다르게 해 20,000개 포트폴리오 생성
# 1. 수익률, 리스크, 비중 list 생성
# 수익률 = port_ret
# 리스크 = port_risk
# 비 중 = port_weights
port_ret = []
port_risk = []
port_weights = []
for i in range(20000):
# 2. 랜덤 숫자 4개 생성 - 랜덤숫자 4개의 합 = 1이되도록 생성
weights = np.random.random(len(stocks))
weights /= np.sum(weights)
# 3. 랜덤 생성된 종목별 비중 배열과 종목별 연간 수익률을 곱해 포트폴리오의 전체 수익률(returns)를 구한다.
returns = np.dot(weights, annual_ret)
# 4. 종목별 연간공분산과 종목별 비중배열 곱하고, 다시 종목별 비중의 전치로 곱한다.
# 결과값의 제곱근을 sqrt()함수로 구하면 해당 포트폴리오 전체 risk가 구해진다.
risk = np.sqrt(np.dot(weights.T, np.dot(annual_cov, weights)))
# 5. 20,000개 포트폴리오의 수익률, 리스크, 종목별 비중을 각각 리스트에 추가한다.
port_ret.append(returns)
port_risk.append(risk)
port_weights.append(weights)
portfolio = {'Returns' : port_ret, 'Risk' : port_risk}
for j, s in enumerate(stocks):
# 6. portfolio 4종목의 가중치 weights를 1개씩 가져온다.
portfolio[s] = [weight[j] for weight in port_weights]
# 7. 최종 df는 시총 상위 5종목의 보유 비중에 따른 risk와 예상 수익률을 확인할 수 있다.
df = pd.DataFrame(portfolio)
df = df[['Returns', 'Risk'] + [s for s in stocks]]
# 8. 효율적 투자선 그래프 그리기
df.plot.scatter(x='Risk', y='Returns', figsize=(10,8), grid=True)
plt.title('Efficient Frontier Graph')
plt.xlabel('Risk')
plt.ylabel('Expected Return')
plt.show()
1. 포트폴리오별 수익률, 리스크, 비중을 담을 빈 LIST를 생성한다.
2. 포트폴리오별 랜덤 가중치 설정
랜덤 숫자 4개 생성 - 랜덤숫자 4개의 합 = 1이되도록 생성
3. 포트폴리오 전체 수익률 returns 구하기
랜덤 생성된 종목별 비중 배열과 종목별 연간 수익률을 곱해 포트폴리오의 전체 수익률(returns)를 구한다.
4.포트폴리오 전체 리스크 risk 구하기
종목별 연간공분산과 종목별 비중배열 곱하고, 다시 종목별 비중의 전치로 곱한다.
결과값의 제곱근을 sqrt()함수로 구하면 해당 포트폴리오 전체 risk가 구해진다.

5. 20,000개 포트폴리오의 수익률, 리스크, 종목별 비중을 각각 리스트에 추가한다.
6. portfolio 4종목의 가중치 weights를 1개씩 가져온다.

7. 최종 df는 시총 상위 5종목의 보유 비중에 따른 risk와 예상 수익률을 확인할 수 있다.
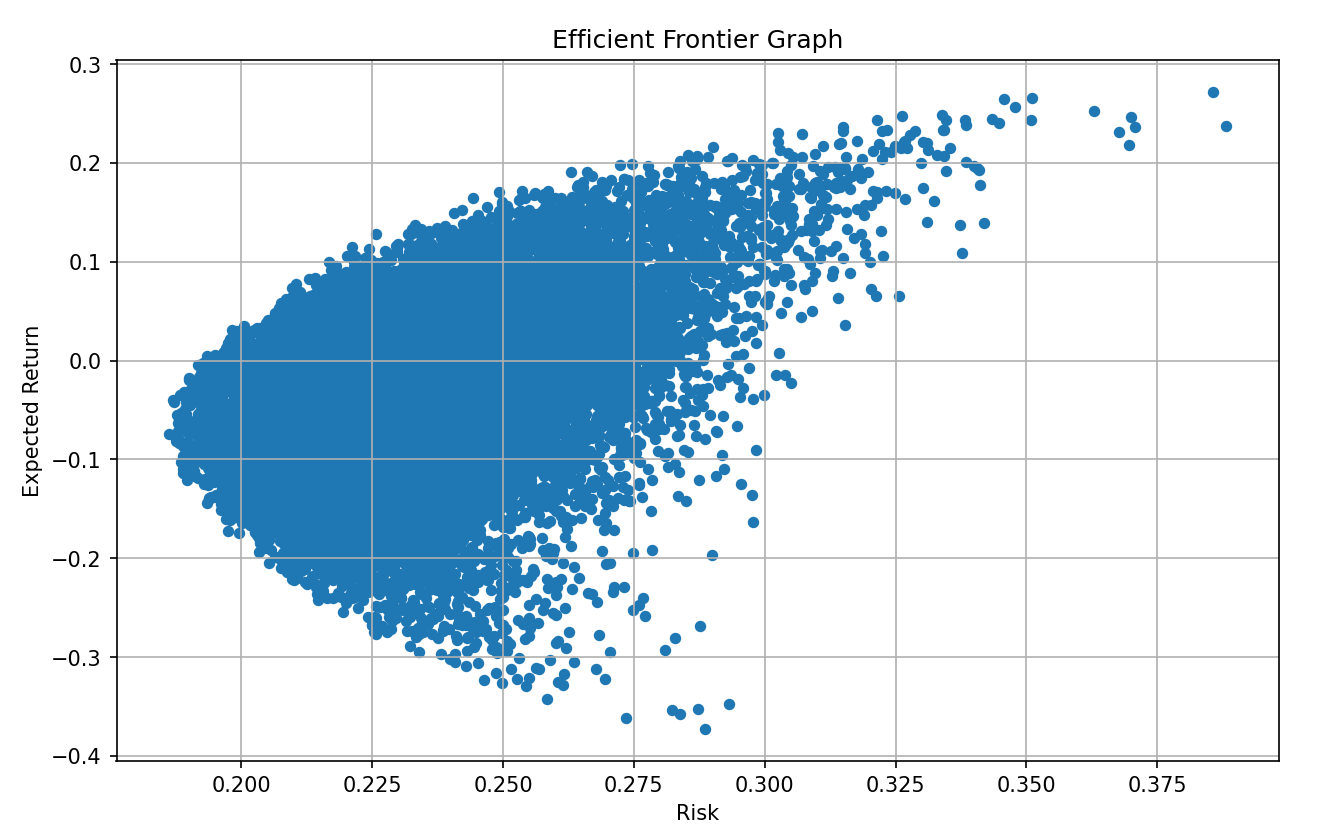
8. 효율적 투자선 그래프 그리기
시가 총액 5순위 5종목에 투자한다고 가정하고 각 종목의 가중치를 임의로 정한 포트폴리오 20,00개를 만들어 그래프로 표시한 결과이다.
x축이 해당 포트폴리오의 리스크이고 Y축이 포트폴리오의 예상 수익률을 나타낸다.
효율적 투자선 전체코드
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 모듈경로 지정
import sys
sys.path.append(r'C:\Users\kwonk\Downloads\개인 프로젝트\juno1412-1\증권데이터분석\DB_API')
# 모듈 가져오기
import Analyzer
mk = Analyzer.MarketDB()
# KOSPI 시가총액 5위
stocks = ['삼성전자', 'LG에너지솔루션', '삼성바이오로직스', 'SK하이닉스', 'LG화학']
# 종목별 일별 시세 dataframe 생성
df = pd.DataFrame()
for i in stocks:
df[i] = mk.get_daily_price(i, '2018-10-13', '2022-12-23')['close']
# 데이터를 토대로 종목별, 일간 수익률, 연간수익률, 일간리스크, 연간리스크를 구하기
# 5종목 일간 변동률
daily_ret = df.pct_change()
# 5종목 1년간 변동률 평균(252는 미국 1년 평균 개장일)
annual_ret = daily_ret.mean() * 252
# 5종목 연간 리스크 = cov()함수를 이용한 일간변동률 의 공분산
daily_cov = daily_ret.cov()
# 5종목 1년간 리스크(252는 미국 1년 평균 개장일)
annual_cov = daily_cov * 252
# 시가총액 5순위 주식의 비율을 다르게 해 20,000개 포트폴리오 생성
# 1. 수익률, 리스크, 비중 list 생성
# 수익률 = port_ret
# 리스크 = port_risk
# 비 중 = port_weights
port_ret = []
port_risk = []
port_weights = []
for i in range(20000):
# 2. 랜덤 숫자 4개 생성 - 랜덤숫자 4개의 합 = 1이되도록 생성
weights = np.random.random(len(stocks))
weights /= np.sum(weights)
# 3. 랜덤 생성된 종목뵹 비중 배열과 종목별 연간 수익률을 곱해 포트폴리오의 전체 수익률(returns)를 구한다.
returns = np.dot(weights, annual_ret)
# 4. 종목별 연간공분산과 종목별 비중배열 곱하고, 다시 종목별 비중의 전치로 곱한다.
# 결과값의 제곱근을 sqrt()함수로 구하면 해당 포트폴리오 전체 risk가 구해진다.
risk = np.sqrt(np.dot(weights.T, np.dot(annual_cov, weights)))
# 5. 20,000개 포트폴리오의 수익률, 리스크, 종목별 비중을 각각 리스트에 추가한다.
port_ret.append(returns)
port_risk.append(risk)
port_weights.append(weights)
portfolio = {'Returns' : port_ret, 'Risk' : port_risk}
for j, s in enumerate(stocks):
# 6. portfolio 4종목의 가중치 weights를 1개씩 가져온다.
portfolio[s] = [weight[j] for weight in port_weights]
# 7. 최종 df는 시총 상위 5종목의 보유 비중에 따른 risk와 예상 수익률을 확인할 수 있다.
df = pd.DataFrame(portfolio)
df = df[['Returns', 'Risk'] + [s for s in stocks]]
# 8. 효율적 투자선 그래프 그리기
df.plot.scatter(x='Risk', y='Returns', figsize=(10,8), grid=True)
plt.title('Efficient Frontier Graph')
plt.xlabel('Risk')
plt.ylabel('Expected Return')
plt.show()
참고도서
http://www.yes24.com/Product/Goods/90578506
파이썬 증권 데이터 분석 - YES24
투자 기법과 프로그래밍 기술로 자신만의 퀀트 투자 시스템을 완성하라『파이썬 증권 데이터 분석』은 웹 스크레이핑으로 증권 데이터를 주기적으로 자동 수집, 분석, 자동 매매, 예측하는 전
www.yes24.com
https://github.com/INVESTAR/StockAnalysisInPython
GitHub - INVESTAR/StockAnalysisInPython
Contribute to INVESTAR/StockAnalysisInPython development by creating an account on GitHub.
github.com
'python > 금융데이터분석' 카테고리의 다른 글
| python 증권데이터 분석 - 볼린저 밴드 지표 python구현 (0) | 2022.12.28 |
|---|---|
| python 증권데이터 분석 - 샤프지수, 포트폴리오 최적화 python구현 (0) | 2022.12.27 |
| python 증권데이터 분석 - 네이버금융 일별 시세 조회 API 만들기 (1) | 2022.12.25 |
| python 증권데이터 분석 - DB Updata 모듈만들기#2, 네이버증권 일별주식시세 DB로 업데이트하기 (0) | 2022.12.25 |
| python 증권데이터 분석 - DB Updata 모듈만들기#1, krx 종목주식시세 DB로 업데이트하기 (0) | 2022.12.24 |



댓글